Up to date
This page is up to date for Blazium 0.4.90 (4.3).
If you still find outdated information, please open an issue.
Vector math
Introduction
This tutorial is a short and practical introduction to linear algebra as it applies to game development. Linear algebra is the study of vectors and their uses. Vectors have many applications in both 2D and 3D development and Blazium uses them extensively. Developing a good understanding of vector math is essential to becoming a strong game developer.
Note
This tutorial is not a formal textbook on linear algebra. We will only be looking at how it is applied to game development. For a broader look at the mathematics, see https://www.khanacademy.org/math/linear-algebra
Coordinate systems (2D)
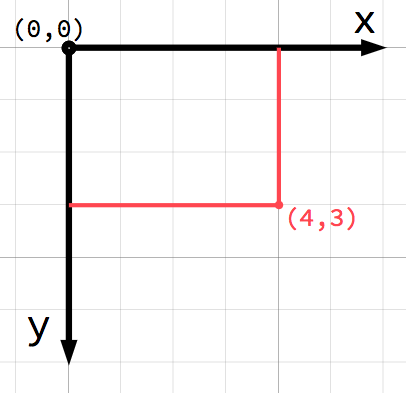
In 2D space, coordinates are defined using a horizontal axis (x) and a
vertical axis (y). A particular position in 2D space is written as a pair of
values such as (4, 3).
Note
If you're new to computer graphics, it might seem odd that the
positive y axis points downwards instead of upwards, as you
probably learned in math class. However, this is common in most
computer graphics applications.
Any position in the 2D plane can be identified by a pair of numbers in this way.
However, we can also think of the position (4, 3) as an offset from the
(0, 0) point, or origin. Draw an arrow pointing from the origin to the
point:
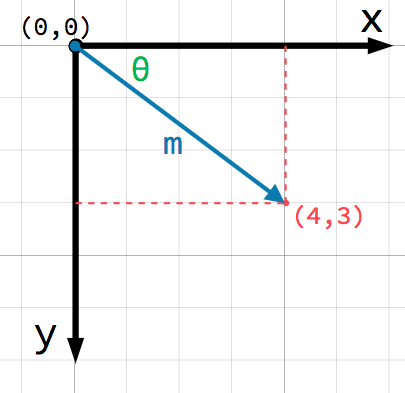
This is a vector. A vector represents a lot of useful information. As well
as telling us that the point is at (4, 3), we can also think of it as an
angle θ (theta) and a length (or magnitude) m. In this case, the arrow
is a position vector - it denotes a position in space, relative to the
origin.
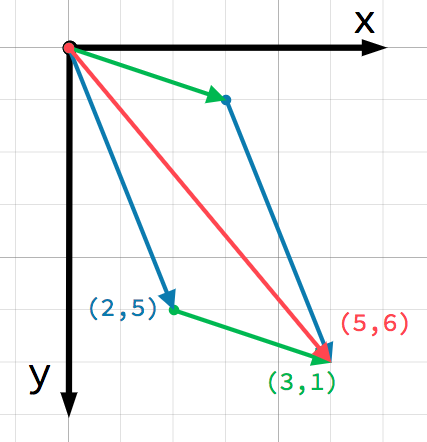
A very important point to consider about vectors is that they only represent relative direction and magnitude. There is no concept of a vector's position. The following two vectors are identical:

Both vectors represent a point 4 units to the right and 3 units below some starting point. It does not matter where on the plane you draw the vector, it always represents a relative direction and magnitude.
Vector operations
You can use either method (x and y coordinates or angle and magnitude) to refer
to a vector, but for convenience, programmers typically use the coordinate
notation. For example, in Blazium, the origin is the top-left corner of the
screen, so to place a 2D node named Node2D 400 pixels to the right and 300
pixels down, use the following code:
$Node2D.position = Vector2(400, 300)
var node2D = GetNode<Node2D>("Node2D");
node2D.Position = new Vector2(400, 300);
Blazium supports both Vector2 and Vector3 for 2D and 3D usage, respectively. The same mathematical rules
discussed in this article apply to both types, and wherever we link to
Vector2 methods in the class reference, you can also check out their
Vector3 counterparts.
Member access
The individual components of the vector can be accessed directly by name.
# Create a vector with coordinates (2, 5).
var a = Vector2(2, 5)
# Create a vector and assign x and y manually.
var b = Vector2()
b.x = 3
b.y = 1
// Create a vector with coordinates (2, 5).
var a = new Vector2(2, 5);
// Create a vector and assign x and y manually.
var b = new Vector2();
b.X = 3;
b.Y = 1;
Adding vectors
When adding or subtracting two vectors, the corresponding components are added:
var c = a + b # (2, 5) + (3, 1) = (5, 6)
var c = a + b; // (2, 5) + (3, 1) = (5, 6)
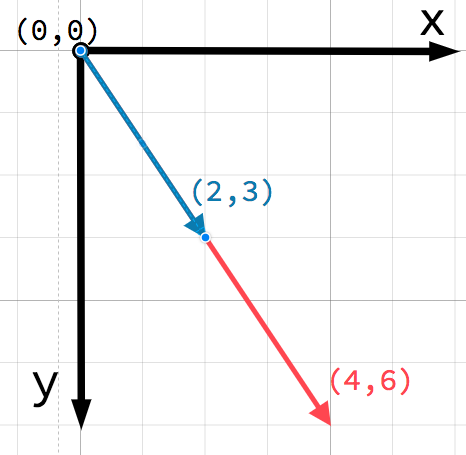
We can also see this visually by adding the second vector at the end of the first:
Note that adding a + b gives the same result as b + a.
Scalar multiplication
Note
Vectors represent both direction and magnitude. A value representing only magnitude is called a scalar. Scalars use the float type in Blazium.
A vector can be multiplied by a scalar:
var c = a * 2 # (2, 5) * 2 = (4, 10)
var d = b / 3 # (3, 6) / 3 = (1, 2)
var e = d * -2 # (1, 2) * -2 = (-2, -4)
var c = a * 2; // (2, 5) * 2 = (4, 10)
var d = b / 3; // (3, 6) / 3 = (1, 2)
var e = d * -2; // (1, 2) * -2 = (-2, -4)
Note
Multiplying a vector by a positive scalar does not change its direction, only its magnitude. Multiplying with a negative scalar results in a vector in the opposite direction. This is how you scale a vector.
Practical applications
Let's look at two common uses for vector addition and subtraction.
Movement
A vector can represent any quantity with a magnitude and direction. Typical
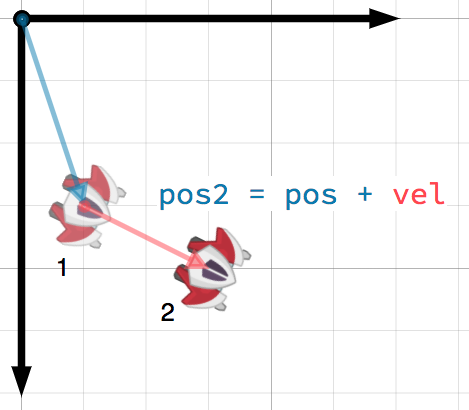
examples are: position, velocity, acceleration, and force. In this image, the
spaceship at step 1 has a position vector of (1, 3) and a velocity vector of
(2, 1). The velocity vector represents how far the ship moves each step. We
can find the position for step 2 by adding the velocity to the current position.
Tip
Velocity measures the change in position per unit of time. The new position is found by adding the velocity multiplied by the elapsed time (here assumed to be one unit, e.g. 1 s) to the previous position.
In a typical 2D game scenario, you would have a velocity in pixels per
second, and multiply it by the delta parameter (time elapsed since
the previous frame) from the _process()
or _physics_process()
callbacks.
Pointing toward a target
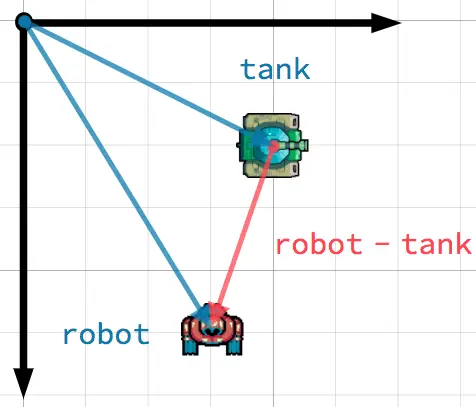
In this scenario, you have a tank that wishes to point its turret at a robot. Subtracting the tank's position from the robot's position gives the vector pointing from the tank to the robot.
Tip
To find a vector pointing from A to B, use B - A.
Unit vectors
A vector with magnitude of 1 is called a unit vector. They are also
sometimes referred to as direction vectors or normals. Unit vectors are
helpful when you need to keep track of a direction.
Normalization
Normalizing a vector means reducing its length to 1 while preserving its
direction. This is done by dividing each of its components by its magnitude.
Because this is such a common operation, Blazium provides a dedicated
normalized() method for this:
a = a.normalized()
a = a.Normalized();
Warning
Because normalization involves dividing by the vector's length, you
cannot normalize a vector of length 0. Attempting to do so
would normally result in an error. In GDScript though, trying to
call the normalized() method on a vector of length 0 leaves the
value untouched and avoids the error for you.
Reflection
A common use of unit vectors is to indicate normals. Normal vectors are unit vectors aligned perpendicularly to a surface, defining its direction. They are commonly used for lighting, collisions, and other operations involving surfaces.
For example, imagine we have a moving ball that we want to bounce off a wall or other object:
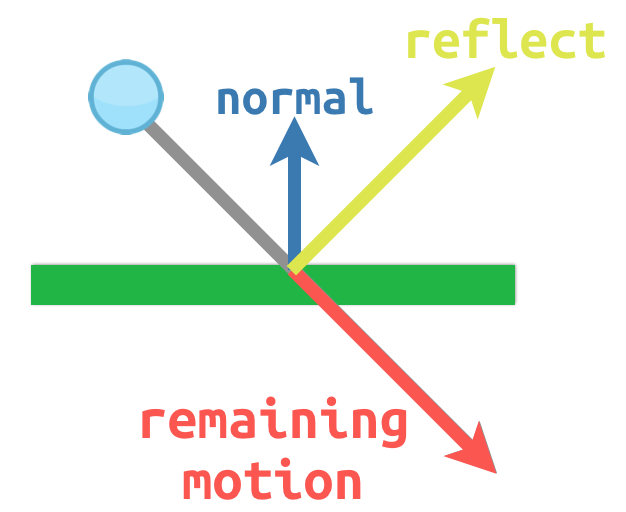
The surface normal has a value of (0, -1) because this is a horizontal
surface. When the ball collides, we take its remaining motion (the amount left
over when it hits the surface) and reflect it using the normal. In Blazium, there
is a bounce() method to handle this.
Here is a code example of the above diagram using a CharacterBody2D:
var collision: KinematicCollision2D = move_and_collide(velocity * delta)
if collision:
var reflect = collision.get_remainder().bounce(collision.get_normal())
velocity = velocity.bounce(collision.get_normal())
move_and_collide(reflect)
KinematicCollision2D collision = MoveAndCollide(_velocity * (float)delta);
if (collision != null)
{
var reflect = collision.GetRemainder().Bounce(collision.GetNormal());
_velocity = _velocity.Bounce(collision.GetNormal());
MoveAndCollide(reflect);
}
Dot product
The dot product is one of the most important concepts in vector math, but is often misunderstood. Dot product is an operation on two vectors that returns a scalar. Unlike a vector, which contains both magnitude and direction, a scalar value has only magnitude.
The formula for dot product takes two common forms:
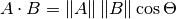
and

The mathematical notation ||A|| represents the magnitude of vector A, and
Ax means the x component of vector A.
However, in most cases it is easiest to use the built-in dot() method. Note that the order of the two vectors does not matter:
var c = a.dot(b)
var d = b.dot(a) # These are equivalent.
float c = a.Dot(b);
float d = b.Dot(a); // These are equivalent.
The dot product is most useful when used with unit vectors, making the first
formula reduce to just cos(θ). This means we can use the dot product to tell
us something about the angle between two vectors:
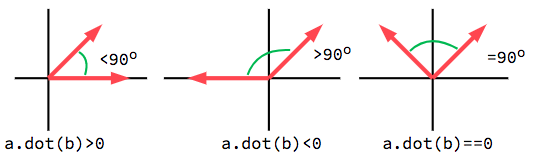
When using unit vectors, the result will always be between -1 (180°) and
1 (0°).
Facing
We can use this fact to detect whether an object is facing toward another
object. In the diagram below, the player P is trying to avoid the zombies
A and B. Assuming a zombie's field of view is 180°, can they see the
player?
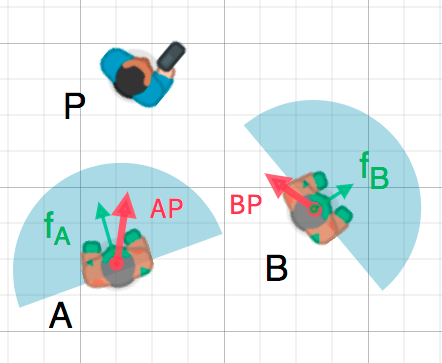
The green arrows fA and fB are unit vectors representing the
zombie's facing direction and the blue semicircle represents its field of view.
For zombie A, we find the direction vector AP pointing to the player
using P - A and normalize it, however, Blazium has a helper method to do this
called direction_to(). If the angle
between this vector and the facing vector is less than 90°, then the zombie can
see the player.
In code it would look like this:
var AP = A.direction_to(P)
if AP.dot(fA) > 0:
print("A sees P!")
var AP = A.DirectionTo(P);
if (AP.Dot(fA) > 0)
{
GD.Print("A sees P!");
}
Cross product
Like the dot product, the cross product is an operation on two vectors. However, the result of the cross product is a vector with a direction that is perpendicular to both. Its magnitude depends on their relative angle. If two vectors are parallel, the result of their cross product will be a null vector.


The cross product is calculated like this:
var c = Vector3()
c.x = (a.y * b.z) - (a.z * b.y)
c.y = (a.z * b.x) - (a.x * b.z)
c.z = (a.x * b.y) - (a.y * b.x)
var c = new Vector3();
c.X = (a.Y * b.Z) - (a.Z * b.Y);
c.Y = (a.Z * b.X) - (a.X * b.Z);
c.Z = (a.X * b.Y) - (a.Y * b.X);
With Blazium, you can use the built-in Vector3.cross() method:
var c = a.cross(b)
var c = a.Cross(b);
The cross product is not mathematically defined in 2D. The Vector2.cross() method is a commonly used analog of the 3D cross product for 2D vectors.
Note
In the cross product, order matters. a.cross(b) does not give the
same result as b.cross(a). The resulting vectors point in
opposite directions.
Calculating normals
One common use of cross products is to find the surface normal of a plane or
surface in 3D space. If we have the triangle ABC we can use vector
subtraction to find two edges AB and AC. Using the cross product,
AB × AC produces a vector perpendicular to both: the surface normal.
Here is a function to calculate a triangle's normal:
func get_triangle_normal(a, b, c):
# Find the surface normal given 3 vertices.
var side1 = b - a
var side2 = c - a
var normal = side1.cross(side2)
return normal
Vector3 GetTriangleNormal(Vector3 a, Vector3 b, Vector3 c)
{
// Find the surface normal given 3 vertices.
var side1 = b - a;
var side2 = c - a;
var normal = side1.Cross(side2);
return normal;
}
Pointing to a target
In the dot product section above, we saw how it could be used to find the angle between two vectors. However, in 3D, this is not enough information. We also need to know what axis to rotate around. We can find that by calculating the cross product of the current facing direction and the target direction. The resulting perpendicular vector is the axis of rotation.
More information
For more information on using vector math in Blazium, see the following articles: